Terms of the Music Theory with Audio Samples

Melody

Sequence of tones that are connected with each other by intervals. In the melody, the tones compare themselves with each other according their pitch. This comparison has a schematized shape: the musical scale. The melodic tones represent degrees of this scale, and the intervals are relations between the degrees. Since the tone ensembles of the keys manifest themselves as scales, the modulation appears as an alteration of the scale degrees.

A melody when sounding together with other melodies is a voice. The aesthetics of the polyphony lies in the forms of the voice leading, which make up the counterpoint.

When a melody reflects its own motion or imitates it in other voices, it is a motif. In regard to the aesthetic structure of the musical categories, the motif is the final basic shape of the sonic going together that characterises the tonal music.

Scale, Scale Degree, Pitch, Whole Tone, Semitone

First of all, the musical scale has the peculiarity that the tones of a key are strung according to their pitch, that is, in an order in which the harmonic coherence of the tones is quite hidden. The tones of the tonic, dominant, and subdominant – in the following recognisable by their harmonic formula – appear very mixed up and are hardly perceptible as what they obviously represent in the cadence. Nevertheless, these harmonies do have their effect so that, in a scale presented as a sequence of tones, the last tone appears as a resolution of the previously accumulated dissonance. The cause of this effect, however, is hidden behind the superficial form of the scale degree motion.

The harmonic difference between major and minor keys appears in the scales as a specific succession of different distances between conjunct degrees. These degree distances result from the harmonic relation between the tonal components, or more specifically: from the external frequency ratios, in which the tonal relations manifest themselves. From the definitions developed in the second chapter, the following "pure" frequency ratios between the degrees can be calculated:

On the basis of the aesthetics of the modulation, the syntonic comma (81:80) between the whole tones 9:8 and 10:9 can be neglected, as is common practice with the equal temperament. Hence, the harmonic structure inherent to the musical scales presents itself as an order in which the minor, major, and augmented second (75:64) – or semitone, whole tone, and, if you will, "one and a half tone" – occur:

In what distances scale degrees occur, is a purely harmonic matter, which is a precondition for the specific order of the scale degrees. Since when singing the tone pitches within a key are hit on the basis of the harmonic intuition, the distances between the degrees can, in practice, be presupposed as given with the utmost naturalness. To some music theorists, this naturalness does not reveal the harmonic basis of the scale degrees, the law of tonality, but rather an arbitrarily arisen tradition preserved by pure imitation, which can and have to be abandoned for the purpose of freeing the music.

The, in the musical scales, schematised pitch level comparison logically does not define what is compared, that is, not tone pitches, but tone degrees. The pitches are already predefined by the tone ensembles of the keys, and that across all audible octave spaces so that they are available as material of an arbitrarily up- and downwardly extendable scale. What characterises the tone degrees itself, is expressed by ordinal numbers: Counted from the tonic root tone, there is a first, second, third etc. level, and these designations refer so solidly to the preconditioned tone relations that they can be used for the description of harmonies. However, that the, in such conventions contained, semblance of a melodic basis of the harmonies is then theoretically taken deadly seriously, is something the degree designations of the chords bear no blame for.

In general, the degrees of the scale are the basis of the intervals.

Compared to the modern scale with seven degrees, the pentatonic scale appears as a scale with two missing tones.

Interval

On the basis of the scale degrees, the harmonic tone relations of the tonality assume a melodic form. They now appear as intervals, whose size is defined by the number of degrees between the tones. According to that, the interval terms are named: Beginning from a random tone lies a further tone

• as a prime on the same level,
• as a second on the next level,
• as a third on the third level,
• as a fourth on the fourth level,
• as a fifth on the fifth level etc.

One can now see the, in melodic ideas based, origin of the names, which also have found its way into the harmonic terminology. By the way, the musical notation is also based on the degree relations of the melodics so that an abstract tone mentioned by name such as the tone A becomes very concrete as soon as it is notated on one or the other stave line.

Intervals distinguish themselves by their size. Sevenths and octaves may differ harmonically as dissonance and consonance; as intervals, they are just different in size. But "size" always means, in the case of intervals, the distance between the tones measured in scale degrees. That is why the minor third and the augmented second are different intervals, "even though", taken by themselves, they sound equally. Also remarkable is the form in which intervals do not differ: All intervals between conjunct degrees are of the same size. Regardless of all harmonic differences, and therefore also regardless of all differences between the minor, major, and augmented second, all seconds correspond as intervals by definition. Just as all thirds, all fourths etc. On that identity of the intervals, all accordance in melodics is based.

Leading Tone

In the opinion of many music theorists, there is supposed to be a tone with the curious property to strive towards another tone. The reason of this property is supposed to be the short distance between the tones: the semitone step between the one, the so-called leading tone, and the other, the target tone. This idea is tautological from the ground up: The interval between two successive tones is supposed to have the capability to cause its own realisation. The occurrence of a tone is supposed to be caused by the relation that it has to the preceding tone, in which relation, however, its occurrence is already logically presupposed. An example for the definition of such a construct:

"Leading tone […], a tone leading to another, stimulating the same one in the expectation, which preferably lies a semitone below the tonic, e.g. B in C major. The step from the leading tone to the target tone is always a minor second … Its forward-directed tendency is melodically to be explained by the small distance to the following tone, harmonically by the belonging to a mostly dominant sound." (Brockhaus Riemann Musiklexikon, Paperback edition 1998)

This definition claims that "the small distance to the following tone" causes a tendency to exactly this following tone. The "target tone" is stimulated "in the expectation" on the basis of a distance that already assumes its existence. The leading tone is the chimera of a tone that tends to carry out a semitone step and has, at the same time, the cause of this tendency in exactly this step. The mention of the tonic and of a harmonic reason cannot hide this absurdity because the harmonic and the melodic are merely considered to be conditions which coincide externally. The semitone step from B to C within the key of C major is not regarded as a melodic form of the harmonic transition from the dominant to the tonic. The harmonic consequence in the occurrence of the tonic as the resolution of a harmonic tension is supposed to be caused directly by the melodic form of this harmonic resolution. The leading tone is a construct that mystifies the law of tonality.

Diatonic scale

The designation of musical scales as 'diatonic' means – grounded in the tradition of modal music – a structure of five whole tones and two semitones. This designation ignores the harmonic reason of modern scales by instead assuming that scales in principle can be formed in any manner from intervals, and that the harmony of the resulting tones takes place more randomly. In this view, the harmonies are not considered as the basis of scale degrees, but, conversely, the scale degrees as a precondition for the formation of harmonies. The existence of a third interval between two consecutive scale degrees, namely the augmented second in a minor key, appears – in the view of this dogmatics – as a deviation from the diatonic scale, which requires a separate explanation: The seventh degree in a minor key is supposedly a distortion of an "original" (diatonically constructed) minor scale, for whose excuse a further fictitious construct is considered to be helpful: the leading tone, which is supposedly required to cause a resolution into the tonic.

Pentatonics, Hemitonic, Anhemitonic, Slendro

The five-step scale (penta = five) stems from the old times when music had no harmonic basis yet. For cultic purposes and for the tuning of the tones of musical instruments, specific tone pitches had to be made binding. The five-step scales seem to be older than the seven-step scales. The number and the position of the tones were a matter of mystical speculation. Observations on the usual singsong were obviously important for the fixation of the tones, which had to achieve a congruence with astrological, religious and other ideas of a holy number. The exact tone relations are different. The tone system of Java (Slendro) is particularly unusual, where the octave was divided almost evenly into five intervals.

The most widespread was a scale, which can be thought of as consisting of four consecutive fifths steps (F-C-G-D-A, or as scale: C-D-F-G-A). In music theory, this scale is named anhemitonic (semitoneless) and is distinguished from the hemitonic scale (with semitones).

Alteration

Alteration is the modification of a scale degree due to a modulation. The transition into a new key is effected by tones that cannot occur in the tone ensemble of the old key. This transition appears on the melodic level as a change of the underlying scale. The old and the new scale may have different root tones, but they have always seven degrees, which are compatible with each other. The accordance of the tonal tone ensembles, in which the harmonic of the modulation lies, appears, for example in the transition from A minor to C major, in the fact that the common tones (C, D, E, F, A, B) lie on the same degrees – in absolute terms, but not relative to the root tone. Thus, even the tones in which the keys differ (G and G sharp) lie on the same degree, namely, on the degree between F and A. Because the scale degrees identify the relative position of the tones within a key. The dispersion of the seven tones across the octave space implies that the tones in which keys differ are close together. G sharp and G have, during the transition from A minor to C major, harmonically nothing to do with one another, but in melodic terms, they lie on the same degree, which, however, is now modified, that is, altered downwards.

Due to the augmented second in the minor scale, there is a special feature of the alteration, as can be seen, for example, in a modulation from A minor to C minor:

The tones G sharp and A flat are tones where both of the tone ensembles of A minor and C minor coincide. From the standpoint of the harmonic perception, the different spelling of these absolutely identical sounding tones seems to be a mere caprice of the notation. This spelling, however, corresponds to the melodic reality according to which G sharp and A flat cannot lie on the same degree in the mentioned keys. Because there is no further degree between G sharp and F in A minor, whereas in C minor, the tone G lies between A flat and F. In return, the A flat is followed by the tone B as an immediately adjoining degree, whereas in A minor, the tone A lies between B and G sharp. The same tones form, according to the respective key, either an augmented second or a minor third. On the basis of the alteration not only can different tones lie on the same degree, but also the same tones on a different degree.

Alteration is the form in which the scale degrees keep their identity even when changing keys. The musical notation is basically appropriate to this fact. However, the use of accidentals and naturals is not restricted to taking into account the essence of the alteration. Writing-technically motivated breaches against the degree logic are known and usual under the term "enharmonic change". Moreover, even harmonically indifferent or atonal passages are notated in a spelling that presupposes the degrees of a scale and therefore the harmonic determinacy of the tones.

The construct of the altered chord is based on a confusion between the harmonic content and the melodic form, as is also typical for the fiction of the leading tone.

Chromaticism

The characteristic of tone sequences that consist of consecutive semitone steps. The tones of the chromatic tone sequence are not something like components of an entirely own, namely chromatic scale, as is commonly believed, but tones of changing keys and their (diatonic) scales. An example for that is the chromatic fugue by Bach, whose theme contains a chromatic tone sequence in which every individual tone belongs to an own harmony so that, whenever the theme sounds, the harmony change also occurs within the bar. In the following section, the theme with the chromatic tone sequence A, B flat, B, C lies in the bass.

J. S. Bach, Chromatic Fugue (BWV 903), bars 140 and 141

In bar 140, the first third makes a transition from A minor (bar 139) to A major. The middle third modulates to F major, and the last third to C major where also bar 141 stays.

Of course, not every chromatic tone sequence has to feature such a markedly harmonic determinacy, in which every tone shows itself to be a component of a specific scale and key. Such tone sequences can also be indifferent or atonal. They can even appear in a form in which not every tone carries weight: The semitone steps can be a mere mediation of a larger tone step and have the effect of a legato. The individual tones of a chromatic sequence may then still be physically identifiable, but, for the perception, they do not appear as tones that have to be taken into account musically. Hence, they do not play any role in the harmonic assignment and can partially be unconsidered for the harmonic analysis.

Accidental, Natural Sign, Key Signature

In Western musical notation, which is based on the seven degrees of the musical scale, the alteration is presented by accidentals: by sharps (#) in order to raise the pitch of a note by one semitone, or by flats (b) in order to lower it accordingly. The raising of a lowered note and, conversely, the lowering of a raised note takes place by a natural sign:

In order to simplify the notation, one writes a complete musical piece in a defined key. Regardless of the fact that the keys in a piece of music usually often change (modulation), one chooses one of the keys that frequently occur in the piece to the key in which the piece is then notated. In the individual bars, one uses only such accidentals that are not covered by the general key signature.

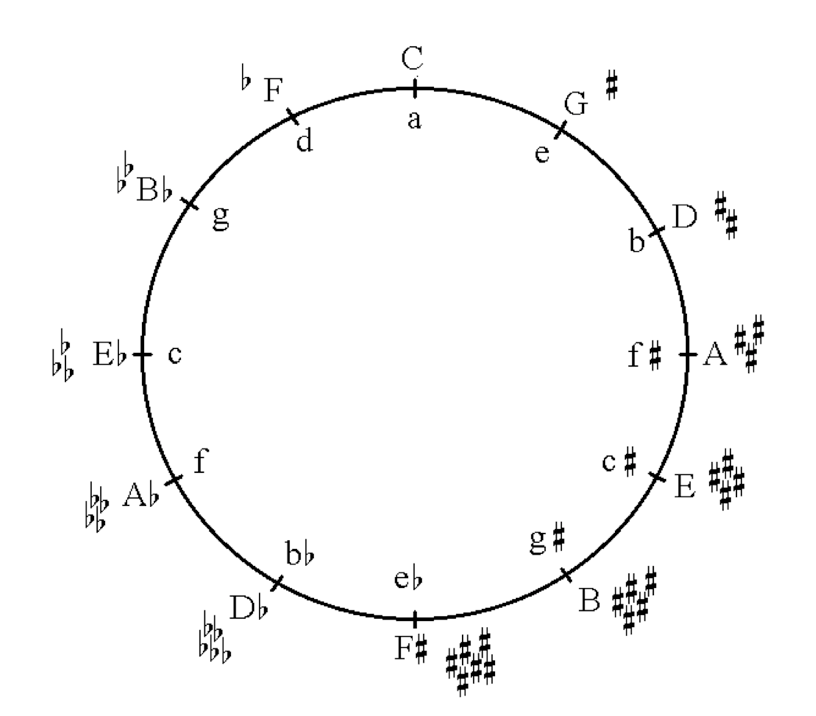
The accidentals have their own logic: One starts with the key of C major and proceeds in each case to the next related key by adding a further accidental. The minor keys have the same accidentals as their closest ("parallel") major key. Therefore, the seventh degree of the minor scale has to be raised in the individual bars. The logic of the accidentals is usually presented in the circle of fifths.

Circle of Fifths

The circle of fifths presents an overview of the accidentals with which a piece of music is assigned a key. Thus, all notes are referred to the key in which the whole piece "stands", and the accidentals directly in front of the notes are only needed in order to indicate the seventh degree in a minor key or the deviations that result from modulations.

Enharmonic Change

The merely writing-technical and for reading more practical exchange of two equally sounding tones. The logic of the accidentals, which is presented by the circle of fifths, is also a convention for writing the keys. According to this convention, one writes a G sharp for the seventh degree of the key of A minor. However, it can be more practical for the presentation of chords or tone sequences to notate the tone G sharp as an A flat. In the system of twelve tones and even more so in the tempered tuning, these are anyhow just different designations for the same tone. This contravention of the logic of the accidentals is called enharmonic change. Often, this is not noticed at all, because only a harmonic analysis shows which keys occur in a piece.

Altered chord

Music textbooks and encyclopaedias usually introduce their readers to a phenomenon which they call “altered chords” and present it something like this:

"Altered chords, since H. Riemann, the designation for such sounds within the functional-harmonic system, in which one or more tones of an originally in-scale chord are chromatically altered ..." (Riemann Musiklexikon, Sachteil, Mainz 1967)

The word "originally" is not meant in terms of time here, as it would be appropriate in the case of the alteration, where in the sequence of the bars a change occurs with the degrees (on the basis of a modulation). Rather, there is talk here of a logical origin: The "in-scale chord" is supposed to be what underlies the "altered chord"; it is supposed to relate to the "altered chord" approximately the same way the pure fifth relates to the tempered fifth. This theory does not notice that in a harmonically determined music all tones – before and after a modulation – belong to a scale anyway, that is, they are "in-scale". Alteration is therefore not understood as a melodic form of the modulation, but as a variation within a key. In this view, harmonies are not judged by their tones, but by the degrees on which the tones can lie. Tones in which two keys differ are then supposed to have anything to do with each other just because they lie on the same degree.