![]()
Terms of the Music Theory with Audio Samples
| Home | Index | Literature | Documents | Contact |
Tonality is the harmony of the key. It exists in the form of the harmonising of a combination of major or minor triads that stand in a fifth relation. As components of this harmony, the consonant triads are called tonic, dominant, and subdominant. The elementary form in which the tonality appears is the cadence. But also the dissonance includes tonal relations insofar as the components of the tonic, dominant, and subdominant sound together inside of it. The tonality, in principle, manifests itself in a sound sequence in which the tones of the tonic, dominant, and subdominant appear together – in whatever form. These seven tones form a harmonic ensemble: the tone ensemble of a key.
The term tonality has been created to designate the harmonious principle of the music based on major and minor keys. (Fétis has introduced this term in order to designate the principle that underlies the relations of the scale tones.) However, from the beginning, nobody spent much time with the analysis and deduction of this harmonic principle of the keys, but instead immediately resolved the category tonality into the abstraction of a meaningful system under which one can imagine all sorts of things. Arnold Schönberg, for example, thought that a more frequent repetition of a tone establishes tonality and that therefore, reversely, the avoidance of such repetitions establishes atonality. Meanwhile, the harmonious characteristic of the tonal relation has disappeared from view so much so that the mere presence of an (indefinite) relation is already accepted as an objective determination. Thus, there is with preference talk of a "relatedness", and the difference between modal and tonal music, which was the point during the concept formation, disappears quite explicitly in the popular definitions of the tonality. Such definitions overlook that harmonic music and harmonic tone relations are quite another matter than the interrelation of ascent, maintaining, and descent in the medieval recitation.
|
|
|
|
|
Tonic, Dominant, Subdominant
Tonic, dominant, and subdominant are the names of three major or minor triads that stand in a fifth relation and, as such, form a harmonic system wherein the tonic stands in the middle, between the upper and lower dominant. The tonal character of these sounds only exists in their combination. The dominant and subdominant have between themselves a relation that stretches across two fifths (9:4), which is mediated and resolved by the tonic.
Usually the term tonic is misunderstood in such a way as if this definition belongs to a triad (or even to a tone) per se. However, the tonic, dominant, and subdominant are reflex categories, that is, determinations that these triads have only by their interrelation and insofar by that harmonic relation which embodies the tonality.
The simple sequence of a tonic, dominant, and subdominant is a cadence, their (partial) together-sounding is a dissonance.
|
|
|
|
|
Sequence of a subdominant, dominant, and tonic (abbreviated: S D T) in the form of consonances. Depending on the order, there are two forms: the authentic form (T S D T)
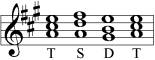
and the plagal form (T D S T)

At the beginning of these examples, the tonic is not yet perceived as such because it has not yet presented itself in relation to the dominant and subdominant. The harmonic character of the tonic reveals itself only at the end of the cadence. It is then perceived as a resolution because it removes the harmonic tension between the dominant and subdominant, in fact, as a sound that underlies this tension as a mediating sound.
|
|
|
|
|
The same sounds which follow each other in the cadence sound together in the dissonance:
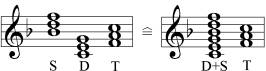
In the case of the above sound sequences, subdominant and dominant are confronted and resolved into the tonic respectively. The harmonic matter is the same. Only the form is different. On the right, the contrast of the dominants occurs as a sound combination and therefore as a dissonance. Hence, the resolution of the contrast between the dominant and subdominant assumes the shape of the resolution of a dissonance.
Thus, the dissonance differentiates from the consonance by the fact that it contains a tonal relation in itself. It is not a combination of immediately harmonising tones, but of tones that harmonise as components of different tonal triads. It is thereby not always necessary that every component of a triad occurs. The dissonance can combine arbitrary parts of the tonic, dominant, and subdominant in itself so that there are a whole series of dissonances, which can be divided into groups depending on their harmonic composition. Here are examples in the key of F major with the related harmonic formula:
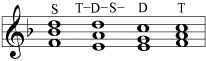
1. Combinations of a dominant and subdominant:

2. Combination of a tonic, dominant, and subdominant in a sound sequence with a resolution into the tonic:
3. Combinations of a tonic and dominant or subdominant:
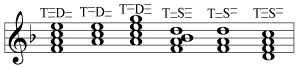
What is referred to as a resolution of a dissonance, is, depending on its tonal characteristic, partly the resolution of the contrast of the dominants (as in the case of the cadence), but also partly the dissolving of the tonic out of the compound with the dominants.
The harmonic differences of the dissonances basically depend on their composition. Regarding their form, they, firstly, have to be distinguished into distinctive dissonances that always reveal their dissonant character taken by itself and, secondly, pseudo consonances. But even distinctive dissonances do not always indicate their harmonic composition taken by itself. This becomes particularly clear when taking a closer look at the frequency ratios in which the sounding-together of the tones of a dissonance results:
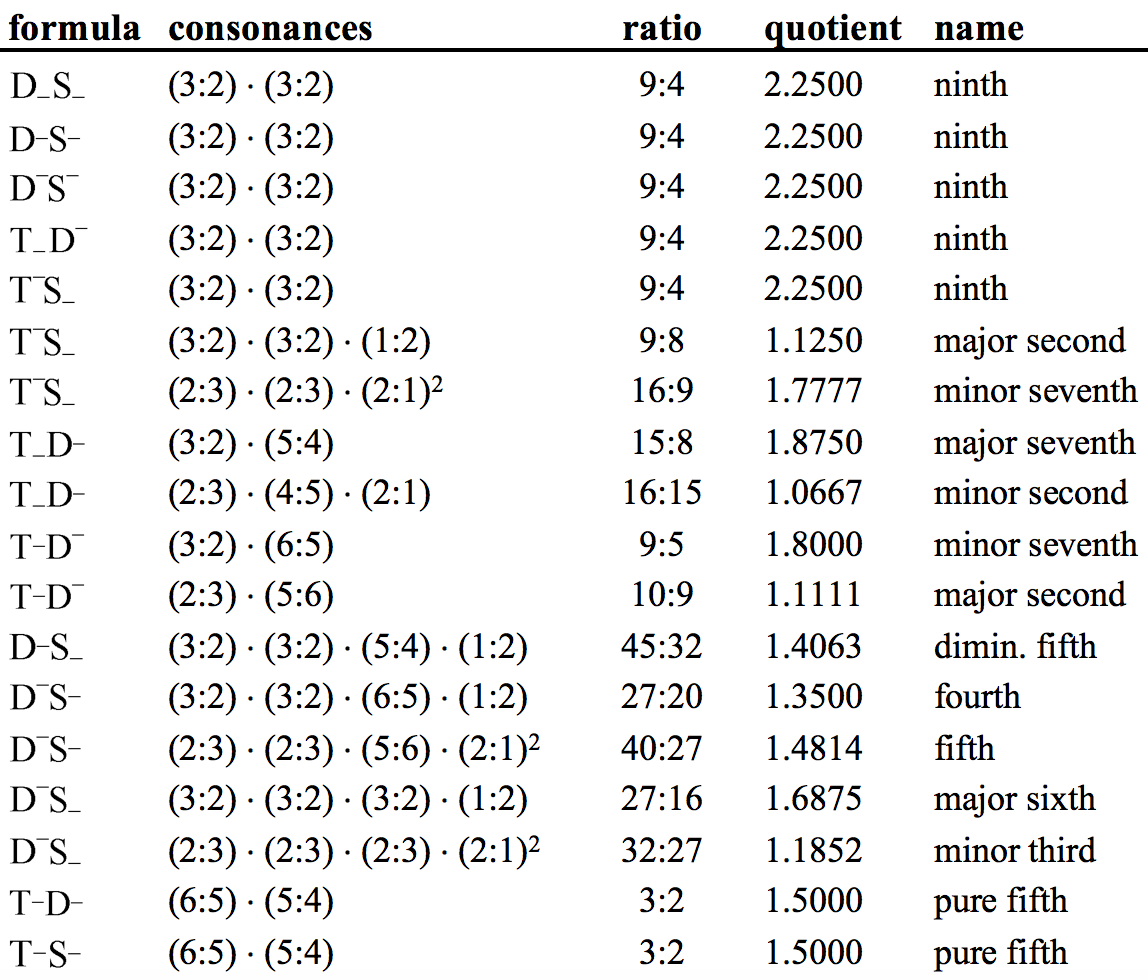
The above examples show
- that different dissonances can have identical frequency ratios,
- that harmonically identical dissonances can have different frequency ratios,
- that different dissonances can, on the basis of their acoustical similarity or sameness, have the same designation.
The frequency ratios in which the harmonic relations present themselves are by no means what constitutes the property of the harmonies. Even the sheer form of the quantitative relation makes any qualitative difference disappear. The relation 16:5 has greater numbers than the relation 9:5 or 6:5, but what does that tell us about the consonance and dissonance? And even the attempt to extrapolate from the pure frequency ratios to the harmony therein manifested can only succeed exceptionally, because of the various possibilities of confusion. Harmonies, by definition, prove to be what they are only in the sequence of sounds in which the confronation of the dominants and the resolution into the tonic takes place. Harmonies are, in substance, components of this tonal movement.
|
|
|
|
|
Frequently occurring dissonance in which the complete dominant sounds together with the root tone of the subdominant. Here an example in the key of F major with the corresponding harmonic formula:

Like all the dissonances, the dominant seventh chord is also resolved into the tonic. The name 'seventh chord' originates from the fact that the tones of the cadence, when arranged in the order of their pitch, turn into the tones of a musical scale. There, the subdominant root tone appears, calculated from the dominant root tone, as the seventh degree. The name thus contains a mixture of the harmonic ("dominant") and the melodic view ("seventh").
|
|
|
|
|
Dissonance of a minor key in which the third and fifth of the dominant sound together with the root tone and third of the subdominant. Here an example in the key of A minor with the related harmonic formula:
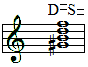
This dissonance is also called seventh chord of the seventh degree.The names of the harmonies are, in principle, not derived from a knowledge of their harmonic composition, but from the melodic idea of the intervals. In this case, the traditional view still circulates that this chord is made up of three minor thirds – one on top of the other, and beginning at the seventh degree of the minor scale – which together form the interval of a seventh diminished by a semitone.
|
|
|
|
|
Dissonance that sounds by itself – that is, outside of its musical context – like a consonance. Its dissonant character and its need for resolution becomes only apparent in sound sequences in which the harmonics of the tonality is effective. Example: The second harmony in this sound sequence:

|
|
|
|
|
It is useful for the harmonic analysis of the dissonances to mark the root tone, third, and fifth as lines behind the abbreviations of the tonic, dominant, and subdominant. The lines symbolise the position of the tones in the basic form of the triad: In this harmonic formula, the root tone is marked at the bottom, the fifth at the top. Example: A combination of the root tones of the dominant and subdominant:
![]()
|
|
|
|
|
The harmonising of the tonic, dominant, and subdominant, which constitutes the tonality, sometimes occurs in pieces of music (often at the beginning or at the end) in the simple form of the cadence, but mostly as a sequence of consonances and dissonances. Thus, the permanent confrontation of the dominants and its resolution into the tonic – or in short: the tonal motion – take place, if one disregards its various movement patterns, by the occurrence of the tones of the tonic, dominant, and subdominant. As such, they bring the harmonic relations of the tonality into effect that determine which key is currently being played. This is also the reason why there are only major and minor keys according to the following scheme:


A major key consists of three major triads, a minor key of two minor triads and one major sound. Major and minor triads can by no means be combined arbitrary into keys. The attempt to assemble three minor triads into a minor key leads, on the basis of the applied tone ensemble, to a pseudo-tonality which consists of pseudo consonances (recognisable by the formulae) and which is resolved into a tonic of a major key:
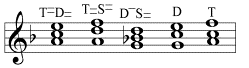
The assertion of the key of F major in the above tone ensemble is based on the stronger consonance of the major triad, whose partial tones have a greater accordance than those of the minor triad. At the beginning of tonality, this still remained undetected: For centuries polyphonic music was made with church modes – that is, with the tone ensemble of the modal music – that prove to be a pseudo-tonality with regard to the harmonic standpoint. It was not until Renaissance music that the G sharp (instead of G) in A minor gradually took hold and the modern keys developed, which in any case have a major triad as a dominant.
By the way, also the attempt to construct a minor tonality by using a major triad as a subdominant will always go awri: It then turns out a pseudo-tonality, which is also resolved by a tonic in a major key.
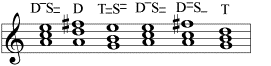
The relationship of the keys is a harmonic fact which is a matter of the modulation.
|
|
|
|
|
| © 2020 Franz Sauter, Hamburg | Data Protection |