![]()
Terms of the Music Theory with Audio Samples
| Home | Index | Literature | Documents | Contact |
In a narrower sense: The going together of elemental sound forms and sonic constellations. In the case of the harmony, it is important what goes well together and why. In this respect, one can distinguish between the going together of tones (consonance, secondly of major and minor triads (tonality), and thirdly of keys (modulation). The harmonics of tonal music has a logical structure: Every basic form of harmony results in a sound shape that is the starting point of the next form of harmonising.
In a broader, also extra-musical sense, harmony means more generally the going together of perceptible things.
Different sound forms are designated closer with the attributes major and minor: tone combinations, keys, and musical scales. The starting point here is the distinction between major and minor triads, which, regarding their basic forms, differ by the positioning of their thirds: The major triad has the minor third (frequency ratio 6:5) above the major one (5:4), the minor triad below it. Derived from this: A major key has a major triad as tonic, a minor key has a minor triad as tonic. Again derived from this: If the tones of a key are ordered according to their pitch, as degree relations, then the result is a scale: a major scale in the case of a major key, a minor scale in the case of a minor key.
Major triad, Root tone, Third, Fifth
A major triad in its basic form consists of a major third and, above it, a minor third, which complete each other to form a fifth. The tones are named root tone, third (now meant as a tone), and fifth. The frequency ratios are shown in the following example:

The frequency ratios in this sound form are:
|
fifth: |
660 Hz : 440 Hz |
= 3:2 |
|
major third: |
550 Hz : 440 Hz |
= 5:4 |
|
minor third: |
660 Hz : 550 Hz |
= 6:5 |
The following illustration includes the partial tones of such a major triad and makes the going together of the tones recognisable, which is characteristic of the consonance of the major triad.
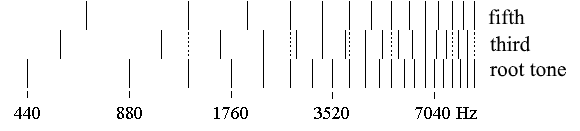
The harmonic difference in comparison to the minor triad lies in this form of the sonic going together.
|
|
|
|
|
A minor triad in its basic form consists of a minor third and, above it, a major third, which complete each other to form a fifth. As with the major triad, the tones are named root tone, third (now meant as a tone), and fifth. The frequency ratios are shown in the following example:

The frequency ratios in this sound form are:
|
fifth: |
660 Hz : 440 Hz |
= 3:2 |
|
major third: |
660 Hz : 528 Hz |
= 5:4 |
|
minor third: |
528 Hz : 440 Hz |
= 6:5 |
The following illustration includes the partial tones of such a minor triad and makes the going together of the tones recognisable, which is characteristic of the consonance of the minor triad.
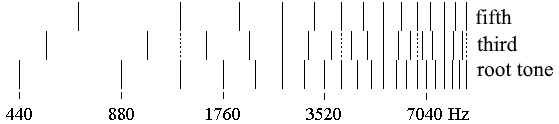
|
|
|
|
|
Harmony of the major and minor triads. The harmony of the consonance is usually very directly attributed to the frequency ratios of the together-sounding tones (2:1, 3:2, 5:4, 6:5) so that the consonance is supposed to be effected by a harmony which lies in the property of numerical ratios. Harmony, however, is a form of the sonic going together. Insofar is the consonance, in the first instance, an immediate going together of the tones. This going together is based on the sound characteristics of the tones, that is, on their composition of partial tones. The still popular idea that harmonic relations are an "imitation" of the "natural" ratios of partial tones turns the reason for the harmony into analogue number ratios. However, harmony does not exist in the relation of the partial tones of one tone, but in the coincidence of the partials of different tones. Heinrich Husmann has presented this fact as the "Coincidence Theory of Consonance".
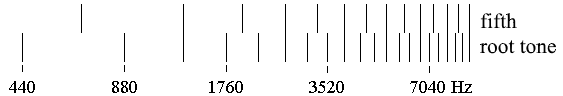
On the basis of the invertibility of the tone combinations, which is based on the consonance of the octave, are the various forms of the major or minor triads also harmonically identical, and because of that are all of them consonant so that consonance in a broader sense means not only an immediate harmonising, but also a sound form that is converted and modified by the consonance of the octave.
|
|
|
|
|
Inversion, Octave
The observation that tone combinations are invertible (discovered by Thomas Campion in 1613) means that a tone when shifted by an octave higher or lower changes only the manifestation of the sound to which it belongs, but not its harmonic character. Therefore are the triads A-C-E and C-E-A harmonically identical. This effect is based on the harmony of the octave, where every partial tone of the higher tone coincides with every second partial tone of the lower tone.
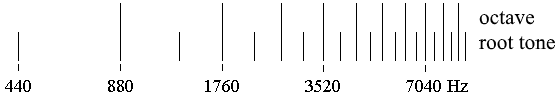
The harmony of the octave is of such a dominance that it contributes little to the harmonic distinction of the tone combinations. Therefore is the fourth E-A only an inversion of the fifth A-E. It has its root tone on top, hence, it is the fifth upside down. The immediate harmonising of the tones in the fourth (4:3) disappears behind the harmony of the fifth (3:2), which, along with the octave (2:1), shapes the harmonic character of the fourth. On this basis are the tones with the frequency ratio 2:1 (octave) on principle harmonically identical, and their identical naming is just the appropriate expression for this fact.

|
|
|
|
|
| © 2020 Franz Sauter, Hamburg | Data Protection |